PWM - en lille historie
under construction.
En PWM udgang er en digital udgang der giver en firkant hvor forhold mellem høj og lav afhænger af den analoge værdi man ønsker at læse ud.
For at laev firkanten om til en analog værdi har man derfor et lavpasfilter på udgangen.
Istedet for at jeg gentager andre så læs:(især den første)
LTSpice - simulering
Jeg har leget lidt med det og brugt LTSpice simuleringsprogrammet der kan downloades gratis
Det er et windows program og skal derfor køre på et windows operativsystem.
(Jeg kører det nu på min ubuntu vha programmet “wine” - det virker fint :-) )
pwm-lp-1ord.asc - et simpelt kredsløb i ltspice
Indgangsignalet er en firkant med længden 0.002 s = 500 Hz
Lidt forklaring:
Et passivt lavpas filter har jo både en indgangsimpedans og udgangsimpedans.
givet et passivt lavpasfilter:
(pwm ud)--(evt buffer1)-->>LP-in---(R)---LP-out--->--(evt buffer2--out)--
|
(C)
|
gnd
håber I kan læse min fine grafik
Indgangsimpedansen er det pwm udgangen ser ud i. Den må ikke være for lav idet den jo så vil belaste udgangen.
Man kan sige at de harmoniske i firkantssignalet(PWM) ser ud i modstanden R idet C er tæt på en kortslutning ved højere frekvenser-
Buffer1 kan den operationsforstærker vi så på idag med 2.5V på minus-ben. Hvis I vil undgå buffer kan I feks sige at R vælges til 1k ohm. SÅ man kan groft sagt max trække 5V/1kohm = 5 mA og det går fint.
Se I i Texas320 noten har de en række eksempler på dimensionering af filtre. Men en PWm frekvens på 10kHz vælger de en knækfrekvens på filtrene på 1000 Hz dvs en faktor 10 fra PWM frekvensen. Som I ser tabel 1er der så megen støjriple tilbage at det med 1. ordens filter svarer til kun små 3 bits opløsning på en DA konverter - altså 8 spændingsniveauer mellem 0 og 5 V idet signalet jo ripler/fluktuerer.
Så skal det være godt kan man
gå noget længere ned med knækfrekvens på det analoge 1. ordens filter. (Istedetfor 500/10 Hz = 50Hz så måske 5 eller 10 Hz)
Eller man skal lave højere ordens filter.
10 Hz filter:
tau = R*C tau = 1 /(2*pi*f) = 1/(2*pi*10) = 0.0159
som giver C = tau/R = 0.0159/1kohm = 1,59 mikro F
Med disse værdier behøves in buffer1.
Til gengæld skal der være en på udgangen (buffer2)
Problemet med en buffer (buffer2) på udgangen er bla rail problemet, at en opamp og en transistor ikke kan give output helt ud til hhv negativ og positiv forsyning.
xxxxxxxxx
Man kan have buffer2 som en simpel npn transistor (feks bc549)
5/12V
|
|/
in-----|
|\
|---- out
|
gnd
Collector vender opad, emitter nedad
Denne buffer virker ok, men har 0.6V mindre på udgang end på indgang pga spændingsfaldet over basis-emitterdioden Dertil kommer at hvis input er mindre end 0.6V går transistoren off.
MAn kan sætte en opamp istedet for med en gangs forstærkning, (Vout koblet til V-minus med en direte forbindelse) men her har man stadig rail problemet.
Problemet er løst hvis man har forsyningsspænding til buffer2 opamp der er større end dynamikområdet (feks ± 12V)
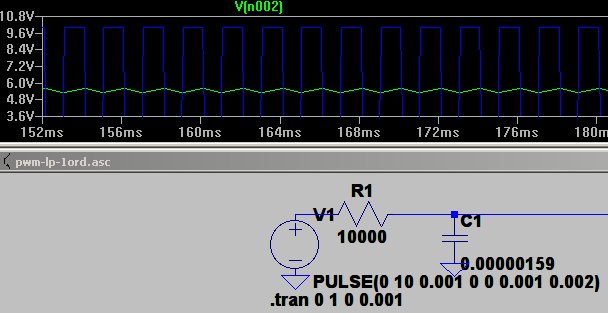
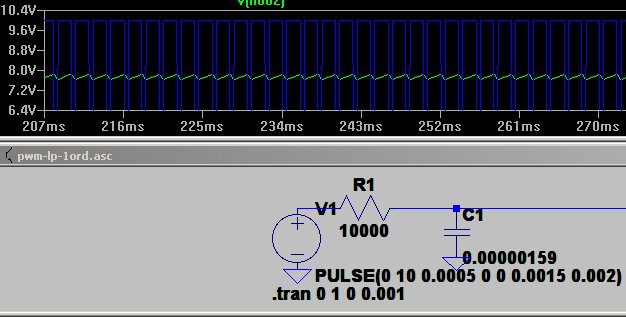
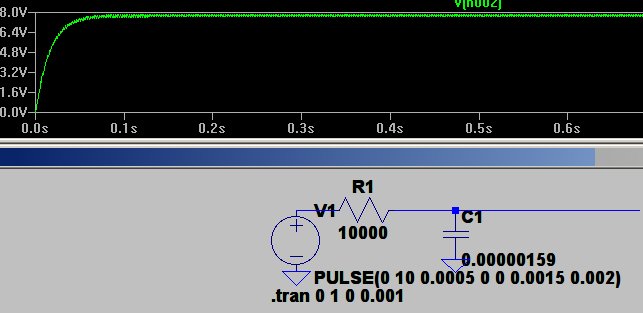
!! Et par eksempler
Et par billeder med 25/75 % og 75/25% frit fra ltspice
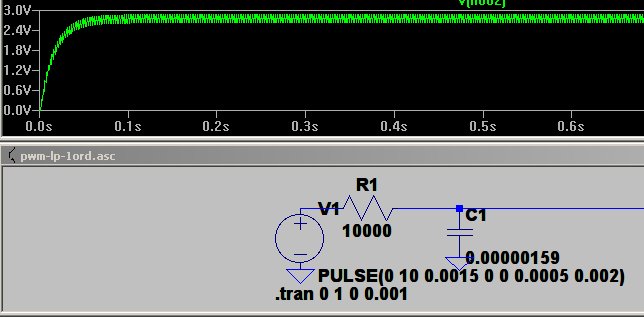 |
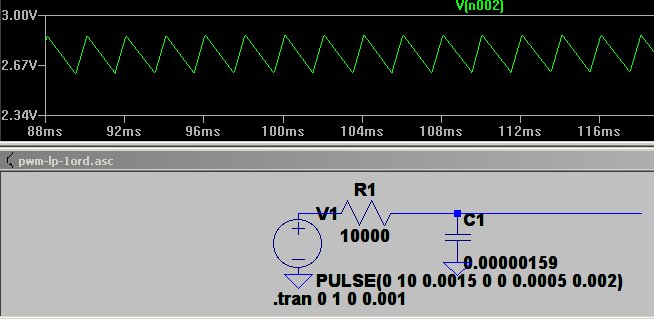 |
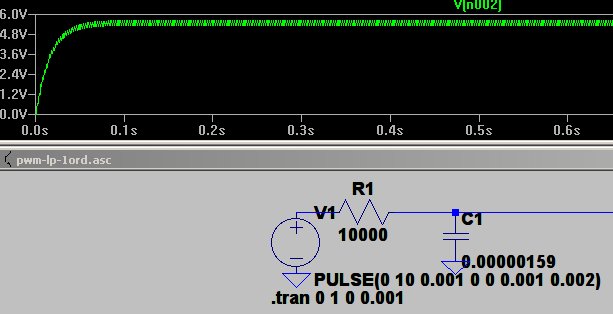 |
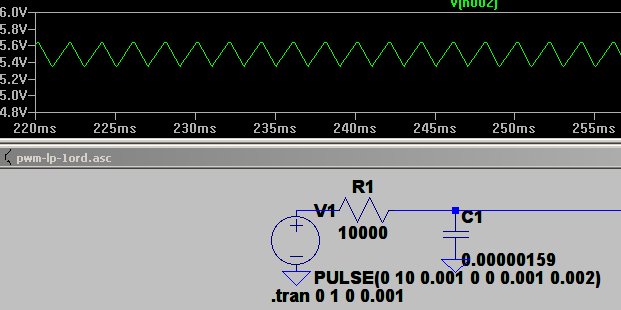 |
 |
 |
 |
