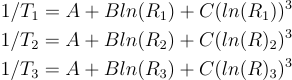# Steinhart-Hart NTC
#https://en.wikipedia.org/wiki/Steinhart%E2%80%93Hart_equation
# https://www.thinksrs.com/downloads/PDFs/ApplicationNotes/LDC%20Note%204%20NTC%20Calculatorold.pdf
# vi har tre sæt målinger af samhørende værdier af R og T:
#

#240820 /JDN

import math
import numpy
import matplotlib.pyplot as plt
# We will find A,B and C coef for the Steinhart-Hart approximation
# We do have three set measurements as seen belo
#  R[Ohm]   temp[C]
# 25415       5
# 10021      25
#  6545     35



# Help functions
# From R to T and T to R
#https://en.wikipedia.org/wiki/Steinhart%E2%80%93Hart_equation

# calc temp from R with use of A,B,C
def calcT(r,abc):
    t = abc[0] + abc[1]*numpy.log(r) + abc[2]*numpy.power(numpy.log(r),3)
    return 1.0/t

# inverse equation calc R from temp given A,B,C

def TtoR(T):  # Temp to Res  [K] !
    xx = (1/abc[2])*(abc[0] - (1/T))
    yy = numpy.sqrt( (abc[1]/(3*abc[2]))**3 + (xx**2)/4)
    return numpy.exp( (yy - xx/2)**(1.0/3.0) - (yy + xx/2)**(1.0/3.0) )

# ----- here we start
# ----- SETUP
# ----- here we start
# ----- SETUP
# ----- here we start
# ----- SETUP

# temp and resistances
TandR = numpy.array([ [5.0 + 273.15, 25415.0],
                     [25.0 + 273.15, 10021.0],
                     [35.0 + 273.15, 6545.0]])

t=numpy.array( [ [1.0/(TandR[0,0])] , [1.0/TandR[1,0]] , [1.0/TandR[2,0]] ] )

# Setting up the matrix with resistances
# Rs * [A,B,C] = (1/temperatures) -> [A,B,C] = inv(Rs) * (1/temps)
#the "Resistor" matrix
#we need to calc ln(R) for the Steimhart formula
a1 = math.log(TandR[0,1])  # log is natural logarithm
a2 = math.log(TandR[1,1])  #
a3 = math.log(TandR[2,1])
m = numpy.array([[1.0,a1, a1**3.],
                 [1.0,a2, a2**3.],
                 [1.0,a3, a3**3.]])

# we need the inverted version of m for finding A,B,C
m_inv=numpy.linalg.inv(m)  # M inverted

#end prepMatricesVectors

# -----
# lets calculate the Steinhart-Hart coefficientsA,B,C  (abc[0],...)

abc = numpy.dot(m_inv,t) # find A,B and C # or   m_inv@t

# and printout
print("Steinhart-Harts parameters A B and C")
print(abc)


#test
t1t = calcT(25415.0,abc)-273.15
t2t = calcT(10021.0,abc)-273.15
t3t = calcT(6545.0,abc)-273.15
print("\ntest estimate temp for 25415 ohm should be 5C: " ,t1t)

print("\ntest estimate temp for 10021 ohm should be 25C:",t2t)

print("\ntest estimate temp for 6545 ohm should be 35C: ",t3t)




# layout of interval for R for plotting
x = numpy.linspace ( start = 1000.    # lower limit
                , stop = 50000.      # upper limit
                , num = 100 )    # generate 100 points

#--------------------

#test with array
Tar = numpy.array([5+273.15,25+273.15,35+273.15])
print("reverse test T to R")
print(TtoR(Tar))
print("res")

Tmany = numpy.linspace ( start = 5+273.15    # lower limit
                , stop = 80. +273.15      # upper limit
                , num = 70)     # generate 100 points
Rmany = TtoR(Tmany)


y = calcT(x,abc)  - 273.15  # This is already vectorized, that is, y will be a vector!              )

#--------------
# plot results

plt.plot( y,x)
plt.plot( calcT(x,abc)  - 273.15,x)
plt.axvline(x = 25, color = 'b' ,label ="25C")
plt.axhline(y = 10021, color = 'r'  ,label = "10021 Ohm")

plt.title("NTC")
plt.ylabel("R[ohm]")
plt.xlabel("T[C]")
plt.grid()
plt.legend(bbox_to_anchor = (1.0, 1), loc = 'upper center')
plt.show()
print("ende")

// http://www.sourcecodesworld.com/source/show.asp?ScriptID=1086

// aug 2024 - Jens Dalsgaard Nielsen
// code for calculating Steinhart-Hart 3rd order approx to NTC
// by three sets of temp(C) and resistance(Ohm) measurements
//
// compile by gcc  gcc findabc.c  -lm
// -lm links math library bq we do use nat log function
//
#include<stdio.h>
#include<stdlib.h>
#include <math.h>

#define matsize 3

float A[matsize][matsize];
float I[matsize][matsize];
float T[matsize];

float R1 = 25415.0,
      R2 = 10021.0,
      R3 = 6545.0,
      T1 = 5.0,
      T2 = 25.0,
      T3 = 35.0;


float ABC[3];

float temp;

void
fillMat ()
{
    A[0][0] = 1.0;
    A[1][0] = 1.0;
    A[2][0] = 1.0;
    A[0][1] = log (R1);  // natural log (ln) 2.71281828
    A[1][1] = log (R2);
    A[2][1] = log (R3);
    A[0][2] = pow (A[0][1], 3.0);
    A[1][2] = pow (A[1][1], 3.0);
    A[2][2] = pow (A[2][1], 3.0);
}

void
invT ()
{
    T[0] = 1.0 / (T1 + 273.15);
    T[1] = 1.0 / (T2 + 273.15);
    T[2] = 1.0 / (T3 + 273.15);
}

void
invA ()
{
    int i, j, k;
    // fill unit matr
    for (i = 0; i < matsize; i++) {
        for (j = 0; j < matsize; j++) {
            if (i == j) {
                I[i][j] = 1;
            } else {
                I[i][j] = 0;
            }
        }
    }
    for (k = 0; k < matsize; k++) {
        temp = A[k][k];
        for (j = 0; j < matsize; j++) {
            A[k][j] /= temp;
            I[k][j] /= temp;

        }
        for (i = 0; i < matsize; i++) {
            temp = A[i][k];
            for (j = 0; j < matsize; j++) {
                if (i == k) {
                    break;
                }
                A[i][j] -= A[k][j] * temp;
                I[i][j] -= I[k][j] * temp;
            }
        }
    }
}

void
calcABC ()
{
    for (int i = 0; i < 3; i++) {
        ABC[i] = 0.0;
        for (int j = 0; j < 3; j++) {
            ABC[i] += I[i][j] * T[j];
        }
    }
}

int
main ()
{
    int i, j, k;

    fillMat ();

    printf ("\n A matrix\n");
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 3; j++) {
            printf ("%.10e	", A[i][j]);
        }
        printf ("\n");
    }

    invT ();
    invA ();
    calcABC ();

    printf ("\n A matrix as unit\n");
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 3; j++) {
            printf ("%.10e	", A[i][j]);
        }
        printf ("\n");
    }

    printf ("\ninv A\n");
    for (i = 0; i < matsize; i++) {
        for (j = 0; j < matsize; j++) {
            printf ("%f	", I[i][j]);
        }
        printf ("\n");
    }

    printf ("\n A B C are\n");
    printf ("\n %.10e %.10e %.10e", ABC[0], ABC[1], ABC[2]);
    printf ("\n---\n");
    return 0;
}